Research

• 

  Ranked Choice Voting and ‘Structural Democracy’

  MGGG

  14 November 2024

  Since 2019, we’ve pursued a major research theme in structural democracy, meaning the study of voting rules and electoral systems in terms of their properties. For example, ranked choice voting is a reform to move away from first-past-the-post voting that’s being debated around the country– but there’s far too little work that models its effects on representation.

  Our work is both theoretical and practical, from building new statistical models of ranking to testing fairness properties across election systems to writing public-facing reports for communities considering a change of election system.

  Here is a selection of projects that the lab has been involved in…

• 

  Recombination and other samplers

  MGGG

  07 November 2024

  Redistricting is the problem of partitioning a set of geographical units into a fixed number of districts, subject to a list of often-vague rules and priorities. In recent years, the use of randomized methods to sample from the vast space of districting plans has been gaining traction in courts of law for identifying partisan gerrymanders, and it was used as an analytical tool by several legislatures and independent commissions.

  The mathematics of sampling graph partitions is interesting in its own right, and there has been enormous progress in recent years. Most of the new methods use an idea that comes from this research group: that spanning trees provide a computationally efficient way to partition a graph, because deleting a single edge cuts the graph into two pieces. We introduced the idea in 2018 and released a supporting software package called GerryChain the same year. Now the spanning tree partition step can be found in several different kinds of samplers, including those introduced by Jonathan Mattingly’s group at Duke and Kosuke Imai’s group at Harvard.

  Here are a few key papers from the lab on samping graph partitions…

• 

  Voting Rights Act Research

  MGGG

  30 November 2022

  The Voting Rights Act of 1965 (or simply the “VRA”) is a landmark law in the United States that centers on ensuring electoral opportunity for minority groups, including those defined by race or by a common language. A key element in bringing a VRA lawsuit is a demonstration of racial polarization in elections — does a minority group tend to vote cohesively for certain “candidates of choice,” but see their choices blocked from election by an also-cohesive majority? Due to the secret ballot, making claims about the racial breakdown of voting patterns requires techniques for statistical inference. Another key element is geography, where plaintiffs must show that the minority group could have made up more than half of a district in a reasonably configured districting plan.

  In the Roberts Court, there has been a steady erosion of VRA precedent and a ratcheting upwards of the burden on plaintiffs to bring a case. We have a research direction looking at possible futures for the VRA, and racial fairness in political representation more broadly.

• 

  Differential Privacy and Redistricting

  MGGG

  24 June 2022

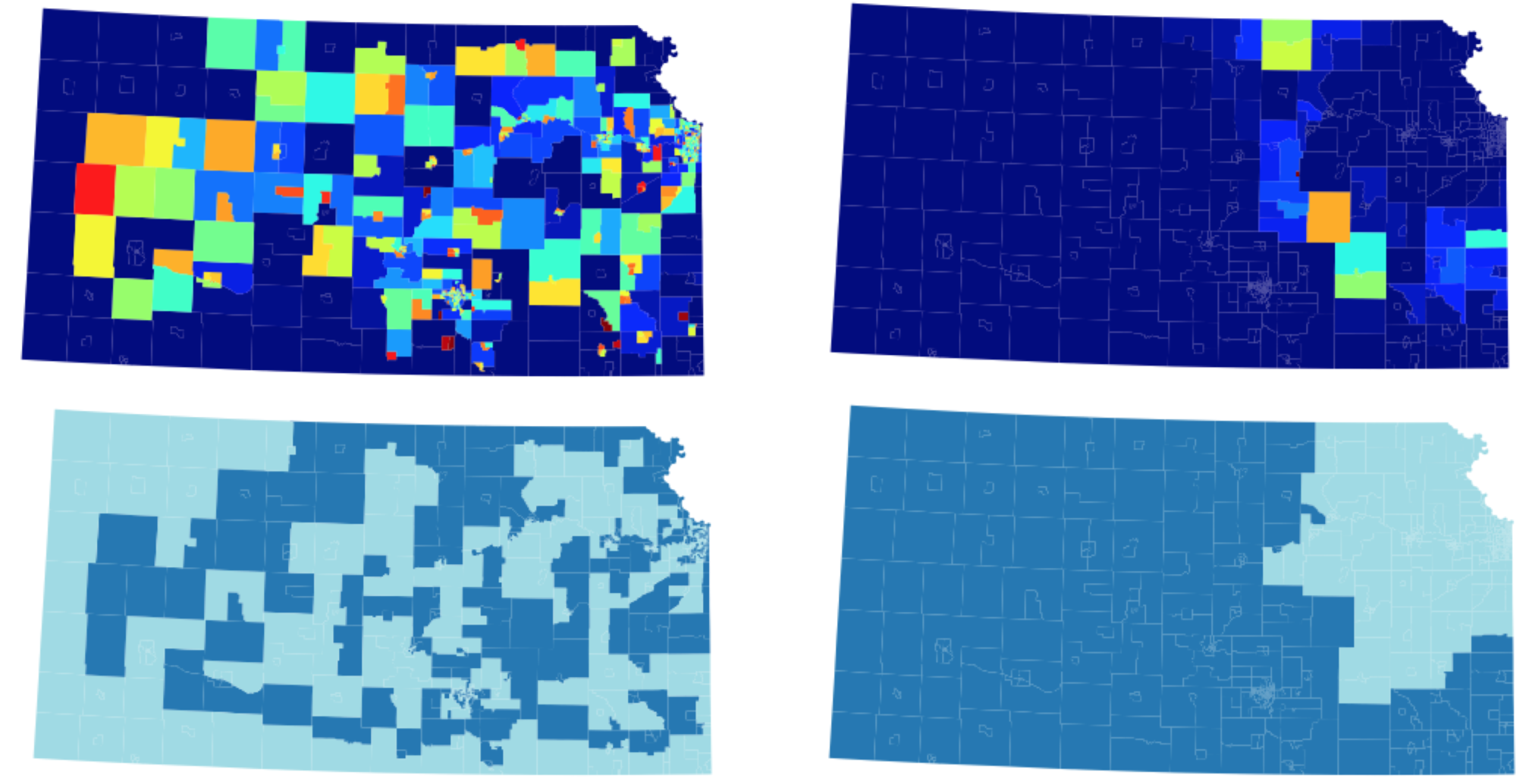
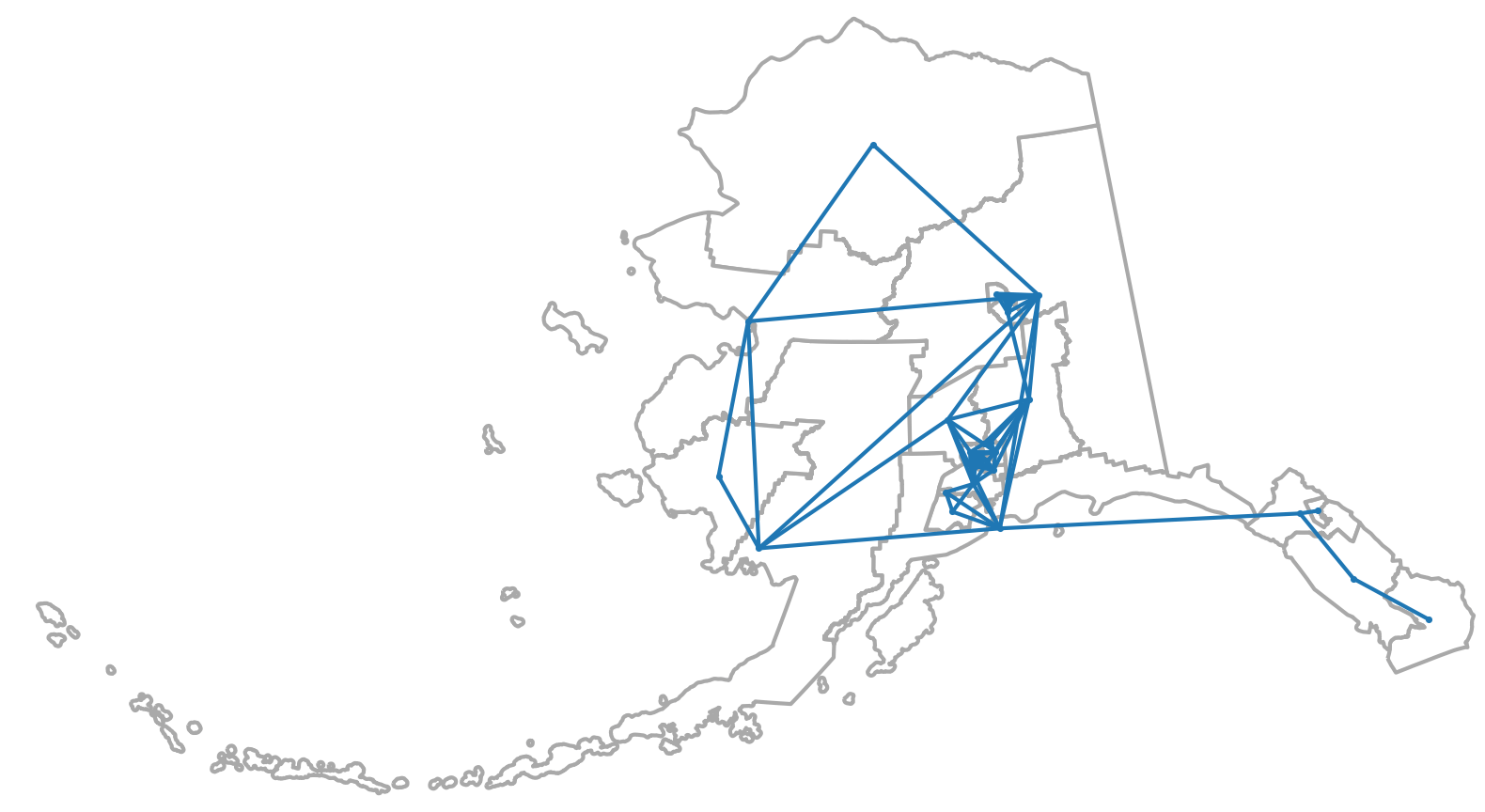
  In order to protect the privacy of individual Census respondents, Census data is released only at aggregate levels, typically combining records for hundreds of individuals or more and just reporting the overall counts. Unfortunately, on its own, this does not provide enough protection to prevent privacy attacks; simple mathematics of linear combinations easily allows people to reconstruct a full individual-level table that is perfectly compatible with the aggregate data.

  To handle this privacy threat, the 2020 Decennial Census was released with a new disclosure avoidance system in place — a differentially private system called TopDown — in order to thwart reconstruction. In short, TopDown adds random noise that cancels out at the aggregate level of cities or districts, but makes individual blocks very noisy.

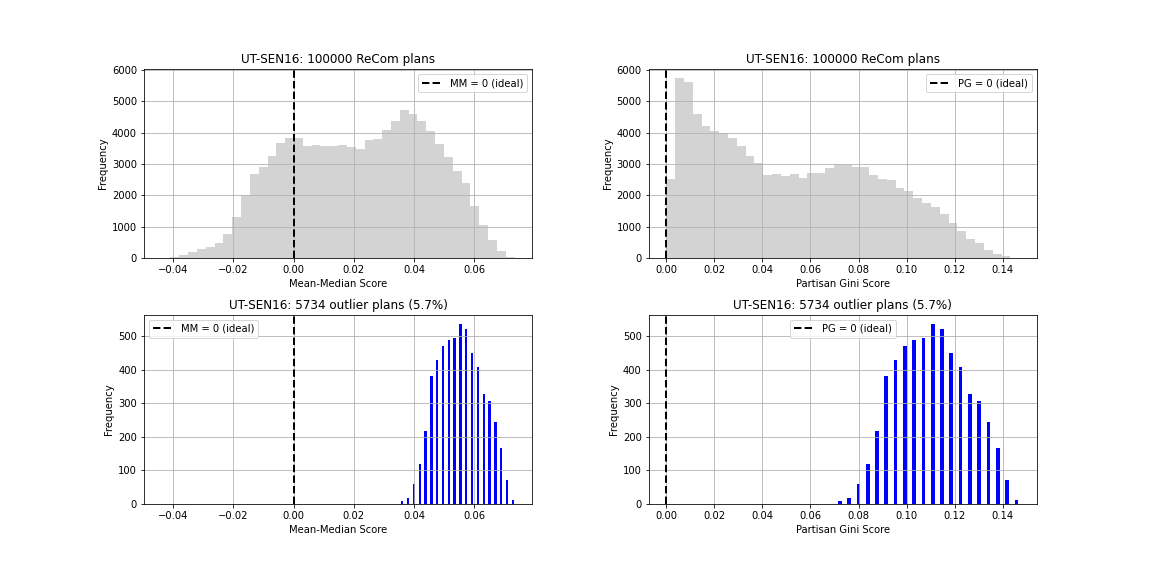
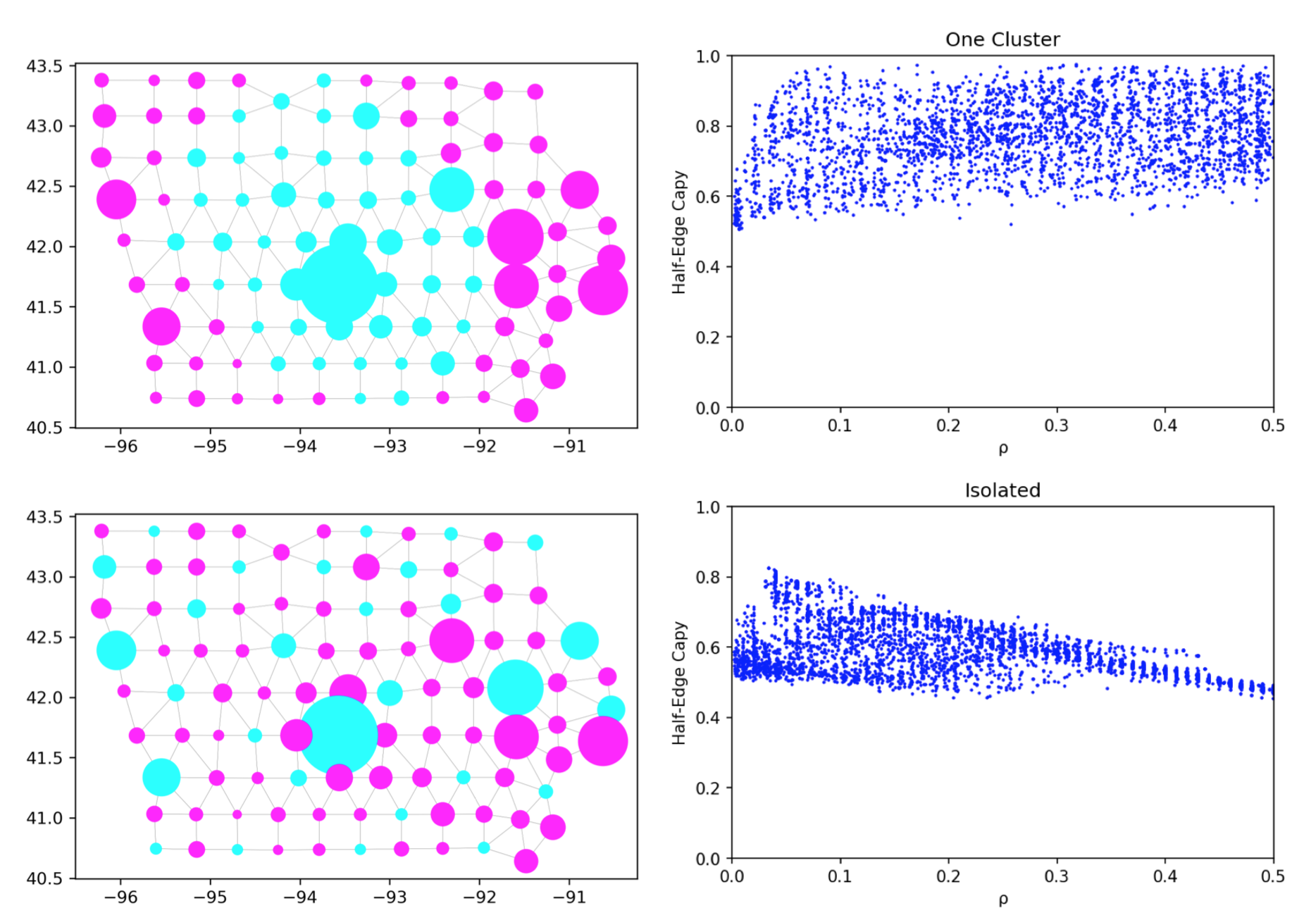
  The Census Bureau released their TopDown code in a public github, but to our knowledge, MGGG was the only group outside of the Bureau to work out how to run it. This enabled several studies that examined whether the noising of Census data would be destructive of its uses for redistricting and voting rights enforcement.

• 

  The (Homological) Persistence of Gerrymandering

  MGGG

  02 October 2020

  We apply persistent homology, the dominant tool from the field of topological data analysis, to study electoral redistricting. Our method combines the geographic information from a political districting plan with election data to produce a persistence diagram. We are then able to visualize and analyze large ensembles of computer-generated districting plans of the type commonly used in modern redistricting research (and court challenges). We set out three applications: zoning a state at each scale of districting, comparing elections, and seeking signals of gerrymandering. Our case studies focus on redistricting in Pennsylvania and North Carolina, two states whose legal challenges to enacted plans have raised considerable public interest in the last few years. To address the question of robustness of the persistence diagrams to perturbations in vote data and in district boundaries, we translate the classical stability theorem of Cohen–Steiner et al. into our setting and find that it can be phrased in a manner that is easy to interpret. We accompany the theoretical bound with an empirical demonstration to illustrate diagram stability in practice.

• 

  Implementing partisan symmetry: Problems and paradoxes.

  MGGG

  02 October 2020

  We consider the measures of partisan symmetry proposed for practical use in the political science literature, as clarified and developed in Katz-King-Rosenblatt. Elementary mathematical manipulation shows the symmetry metrics derived from uniform partisan swing to have surprising properties. To accompany the general analysis, we study measures of partisan symmetry with respect to recent voting patterns in Utah, Texas, and North Carolina, flagging problems in each case. Taken together, these observations should raise major concerns about using quantitative scores of partisan symmetry – including the mean-median score, the partisan bias score, and the more general “partisan symmetry standard” – as the decennial redistricting approaches.

• 

  Clustering propensity: A mathematical framework for measuring segregation

  MGGG

  02 October 2020

  We propose a new family of metrics called capy (or clustering propensity) scores, designed to measure the clustering level of one or more subgroups within a population. The intended application is to offer new ways of measuring the segregation of demographic subgroups. We discuss two main capy scores, Edge and HalfEdge (as well as weighted variants of each) and we compare them to existing segregation scores in the political science, geography, and network science literature. To evaluate the scores, we compute and plot values of minority proportion ρ vs. clustering score C for test distributions on large n × n grids, and on actual demographic data from U.S. states and cities. We argue that capy scores successfully discern qualitatively important differences while providing a stabler baseline for interpretation than classic scores like the Dissimilarity Index and Moran’s I.

• 

  Geometry of Graph Partitions via Optimal Transport

  Tara Abrishami, Nestor Guillen, Parker Rule, Zachary Schutzman, Justin Solomon, Thomas Weighill, and Si Wu

  17 December 2019

  We define a distance metric between partitions of a graph using machinery from optimal transport. Our metric is built from a linear assignment problem that matches partition components, with assignment cost proportional to transport distance over graph edges. We show that our distance can be computed using a single linear program without precomputing pairwise assignment costs and derive several theoretical properties of the metric. Finally, we provide experiments demonstrating these properties empirically, specifically focusing on its value for new problems in ensemble-based analysis of political districting plans.

• 

  Complexity and Geometry of Sampling Connected Graph Partitions

  Daryl DeFord, Lorenzo Najt, and Justin Solomon

  17 December 2019

  In this paper, we prove intractability results about sampling from the set of partitions of a planar graph into connected components. Our proofs are motivated by a technique introduced by Jerrum, Valiant, and Vazirani. Moreover, we use gadgets inspired by their technique to provide families of graphs where the “flip walk” Markov chain used in practice for this sampling task exhibits exponentially slow mixing. Supporting our theoretical results we present some empirical evidence demonstrating the slow mixing of the flip walk on grid graphs and on real data. Inspired by connections to the statistical physics of self-avoiding walks, we investigate the sensitivity of certain popular sampling algorithms to the graph topology. Finally, we discuss a few cases where the sampling problem is tractable. Applications to political redistricting have recently brought increased attention to this problem, and we articulate open questions about this application that are highlighted by our results.

• Measuring Competitiveness

  MGGG

  15 October 2019

  What is a competitive election, anyway? At first it may sound like an obvious question, but it turns out to be hard to specify. Even more subtle is to figure out what exactly we might mean by saying that one districting plan is more competitive than another.

• 

  Mathematics of Nested Districts: The Case of Alaska

  MGGG

  07 June 2019

  This paper analyzes a pairing rule that eight states require of their state legislative districting plans—that state Senate districts must be formed by joining adjacent pairs of House districts. From a mathematical perspective, this is a question of constructing perfect matchings on the dual graph of the House districts.

• 

  Locating the representational baseline: Republicans in Massachusetts

  M. Duchin, T. Gladkova, E. Henninger-Voss, B. Klingensmith, H. Newman, and H. Wheelen

  22 October 2018

  We argue that the underperformance of Republicans in Massachusetts is not attributable to gerrymandering, nor to the failure of Republicans to field House candidates, but is a structural mathematical feature of the distribution of votes. For several of the elections studied here, there are more ways of building a valid districting plan than there are particles in the galaxy, and every one of them will produce a 9-0 Democratic delegation.

• Total variation isoperimetric profiles

  D. DeFord, H. Lavenant, Z. Schutzman, and J. Solomon

  21 September 2018

  An investigation of multi-scale compactness scores.

• Discrete geometry for electoral geography

  M. Duchin and B. Tenner

  15 August 2018

  An overview of problems with “compactness” and a call for research on discrete scores.

• Gerrymandering and Compactness: Implementation Flexibility and Abuse

  R. Barnes and J. Solomon

  07 March 2018

  Sensitivity analysis of compactness scores.

• Medium-scale curvature for Cayley graphs

  A. Bar-Natan, M. Duchin, and R. Kropholler

  07 December 2017

  A pure math riff on an idea for gerrymandering: can we use Ricci curvature to detect natural clusters in the dual graphs of states and other jurisdictions?